Analyzing Profits and Losses Through the Lens of the Average Cost Curve: Implications for Business Decision-Making"
Profits and Losses with the Average Cost CurveAnalyzing Profits and Losses Through the Lens of the Average Cost Curve: Implications for Business Decision-Making"
Does maximizing profit (producing where MR = MC) imply an actual economic profit? The answer depends on the relationship between price and average total cost. If the price that a firm charges is higher than its average cost of production for that quantity produced, then the firm will earn profits. Conversely, if the price that a firm charges is lower than its average cost of production, the firm will suffer losses. You might think that, in this situation, the farmer may want to shut down immediately. Remember, however, that the firm has already paid for fixed costs, such as equipment, so it may continue to produce and incur a loss. Figure 8.5 illustrates three situations: (a) where price intersects marginal cost at a level above the average cost curve, (b) where price intersects marginal cost at a level equal to the average cost curve, and (c) where price intersects marginal cost at a level below the average cost curve.First consider a situation where the price is equal to $5 for a pack of frozen raspberries. The rule for a profit-maximizing perfectly competitive firm is to produce the level of output where Price = MR = MC, so the raspberry farmer will produce a quantity of 90, which is labeled as E in Figure 8.5 (a). Remember that the area of a rectangle is equal to its base multiplied by its height. The farm’s total revenue at this price will be shown by the larger rectangle starting from the origin right to a quantity of 90 packs (the base) up to point E (the height), left to the price of $5, and back down to the origin. The average cost of producing 90 packs is shown by point C or about $3.50. Total costs will be the quantity of 90 times the average cost of $3.50, which is shown by the area of the rectangle from the origin to a quantity of 90, up to point C, over to the vertical axis and down to the origin. It should be clear from examining the two rectangles that total revenue is greater than total cost. Thus, profits will be the blue shaded rectangle on top. It can be calculated as: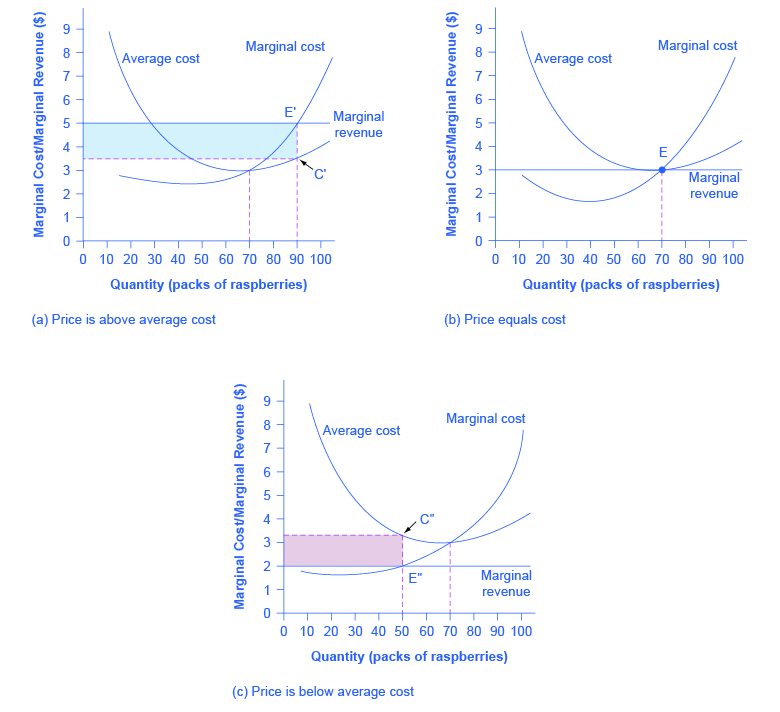
Figure 8.5. Price and Average Cost at the Raspberry Farm In (a), price intersects marginal cost above the average cost curve. Since price is greater than average cost, the firm is making a profit. In (b), price intersects marginal cost at the minimum point of the average cost curve. Since price is equal to average cost, the firm is breaking even. In (c), price intersects marginal cost below the average cost curve. Since price is less than average cost, the firm is making a loss.
| profit | = | total revenue − total cost |
| = | (90)($5.00) − (90)($3.50) | |
| = | $135 |
| profit | = | (price − average cost) × quantity |
| = | ($5.00 − $3.50) × 90 | |
| = | 135 |
| profit | = | total revenue − total cost |
| = | (70)($3.00) − (70)($3.00) | |
| = | $0 |
| profit | = | (price − average cost) × quantity |
| = | ($3.00 − $3.00) × 70 | |
| = | $0 |
| profit | = | total revenue − total cost |
| = | (50)($2.00) − (50)($3.30) | |
| = | -$65.00 |
| profit | = | (price − average cost) × quantity |
| = | ($1.75 − $3.30) × 50 | |
| = | -$65.00 |
| Table 8.4 | ||
|---|---|---|
| If… | Then… | |
| Price > ATC | Firm earns an economic profit | |
| Price = ATC | Firm earns zero economic profit | |
| Price < ATC | Firm earns a loss | |
Self Check: Profit and Losses in Competitive Markets
Our Advantages
- Quality Work
- Unlimited Revisions
- Affordable Pricing
- 24/7 Support
- Fast Delivery
Order Now